2509. The post office
To prepare for the final stage of the European Code
Challenge, the organizers needed to send n items to the event location. For each item, its mass in grams mi is known.
For shipping, they decided to use the postal service “Superexpress”. The service
accepts parcels, each of which may contain one or several items. The mass of a
parcel is equal to the sum of the masses of all items placed inside it.
Sending a parcel costs euro per gram, except for
parcels that fall under a special offer: if a parcel weighs exactly one
kilogram, the cost of sending it is p euros.
The organizers of the European Code Challenge want to send
all items while spending as little money as possible. Help them distribute the
items among the parcels so as to minimize the total shipping cost.
Input. The first line contains two integers n and p (1 ≤ n ≤ 14; 1 ≤ p ≤ 1000) – the number of items and
the shipping cost of a parcel under the special offer.
The second line contains n
integers m1, m2, ..., mn (1 ≤ mi
≤ 1000 for all i from 1 to n).
Output. Print one number – the
minimum total cost of shipping all items (in euros).
|
Sample
input |
Sample
output |
5 800
100 200 300
400 500 |
1300 |
SOLUTION
dynamic
programming – the masks
Algorithm analysis
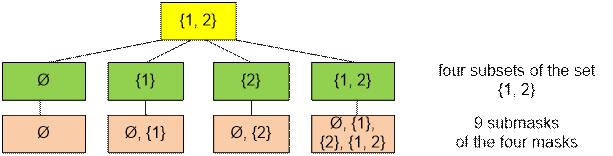
Let’s
introduce the notion of a mask that represents a subset of items to be
shipped. For example, the mask mask = 5 = 1012 specifies the subset containing the 0-th and 2-nd items (items are
numbered from zero).
For
each subset, we compute its total weight, which determines the shipping cost.
If this weight is exactly 1000 grams, then since p ≤ 1000, it is
always beneficial to use the special offer.
Let
MinCost[mask] denote the minimum cost (in euros) of shipping the subset
of items represented by mask. Then for any mask x that is a
subset of mask, the following relation holds:
MinCost[mask] = ![]()
Since the mask 2n – 1 corresponds
to the entire set of n items, the answer to the problem will be the
value MinCost[2n
– 1].
Theorem.
Enumerating all masks and all of their submasks takes O(3n) time.
Proof 1. Consider
the i-th bit. There are three possible cases for it:
·
it is included in the mask mask and included
in the submask sub;
·
it is included in the mask mask but not
included in the submask sub;
·
it is included in neither the mask mask nor the
submask sub;
There are n bits in total, so the total number
of different combinations is 3n.
Proof 2. Let a mask mask contain k set bits. Then it has exactly 2k submasks.
The number of masks of length n with exactly k set bits is ![]() . Therefore, the total number of combinations is
. Therefore, the total number of combinations is
 = (1 + 2)n = 3n
= (1 + 2)n = 3n
Algorithm implementation
We’ll store the item
weights in the array m. In the cell MinCost[mask], we’ll store
the minimum shipping cost for the subset of items represented by the mask mask.
int m[15], MinCost[1 << 14];
Read the input data.
scanf("%d %d",&n,&p);
for (i = 0; i <
n; i++) scanf("%d",&m[i]);
In the variable mask, iterate over all possible
masks from 0 to 2n
– 1.
for (mask = 0; mask
< (1 << n); mask++)
{
Store in the variable Cost the total weight of the
subset of items corresponding to the mask mask. To do this, examine the
binary representation of mask: if the bit at position i is 1,
then add the weight of the i-th item to Cost.
for (Cost = i = 0; i
< n; i++)
if (mask
& (1 << i)) Cost += m[i];
If the value of Cost is strictly equal to 1000,
then since the problem states that p ≤ 1000, assign the value p to
Cost.
if (Cost ==
1000) Cost = p;
Store the computed shipping cost in the corresponding cell
of the MinCost array.
MinCost[mask] = Cost;
}
For each mask mask, iterate over all subsets x Ì mask
(the mask x is a subset of mask if and only if mask AND x
equals x). If we subtract the set corresponding to x from the set
corresponding to mask, we get the set with mask mask XOR x.
For example, if mask = 11012 and x = 10012, then mask XOR x = 1002, which corresponds to the
set-theoretic operation {1, 3, 4} \ {1, 4} = {3}.
for (mask = 0; mask
< (1 << n); mask++)
for (x = 0; x <
mask; x++)
Recompute the value of MinCost[mask] according to
the recurrence relation given in the problem analysis.
if ((mask & x) == x)
MinCost[mask] = min(MinCost[mask],MinCost[mask^x] + MinCost[x]);
Print
the answer, which is stored in the cell MinCost[2n – 1].
printf("%d\n",MinCost[(1
<< n) - 1]);
Algorithm implementation with
complexity O(3n)
Declare
the constant and the arrays.
#define MAX 0xFFFFFFFF
unsigned int
m[15], MinCost[1 << 14];
For a mask mask, it is necessary to iterate over
all its submasks sub and find the minimum among all possible values
FindCost(sub) + FindCost(mask ^ sub)
Due to the symmetry of this sum, it is sufficient to
consider only those submasks sub for which the condition sub ≥ mask ^ sub holds.
unsigned int
FindCost(int mask)
{
if
(MinCost[mask] != MAX) return MinCost[mask];
// sub ïåðåáèðàåò
âñå ïîäìàñêè ìàñêè mask
for (int sub = (mask - 1) & mask;
sub >= mask ^ sub; sub = (sub -
1) & mask)
MinCost[mask] =
min(MinCost[mask], FindCost(sub) + FindCost(mask ^ sub));
return
MinCost[mask];
}
The main part of the program. Set MinCost[mask] =
-1 for all masks whose shipping cost for the corresponding set of items has not
yet been computed.
memset(MinCost,0xFF,sizeof(MinCost));
Read the input data.
scanf("%d %d",&n,&p);
for(i = 0; i < n; i++) scanf("%d",&m[i]);
If the cost of a certain subset of items does not exceed 1000
(specifically, not more, not less, since the case p = 1000 is possible), then the special offer cannot be applied to their
shipment. For such subsets, MinCost[mask] can be immediately computed as
the sum of the costs of all items. If the sum of item costs is exactly 1000,
then we assign MinCost[mask] = p.
Thus, we preliminarily fill in the known minimum costs for
small subsets. This increases the efficiency of the program.
for (mask = 0; mask < (1 << n);
mask++)
{
for(Cost = i
= 0; i < n; i++)
if (mask
& (1 << i)) Cost += m[i];
if (Cost ==
1000) Cost = p;
if (Cost
<= 1000) MinCost[mask] = Cost;
}
Print the answer. The entire set of items is represented
by the mask 2n
– 1, whose binary representation consists of n ones.
printf("%u\n",FindCost((1
<< n) - 1));